Sehr geehrter Herr Manger!

Um mein schlechtes Gewissen etwas zu beruhigen, habe ich letztes Wochenende Ihre Lautsprecher theoretisch etwas durchleuchtet. Zu meiner Überraschung stellte sich dabei heraus, dass das von Ihnen gewählte Abstrahlprinzip zumindest in der von mir untersuchten Idealisierung ein zu jedem Zeitpunkt dem Strom entsprechende Abstrahlung ergibt; d.h. das Einschwingvorgänge und ähnliche störende Effekte nicht auftreten.

Wenn ich die Gleichungen richtige deute, so erscheint es denkbar, dass ein Platte (Membran), deren Steife von innen nach außen allmählich abnimmt (Dickenänderung), zu einem besseren Wirkungsgrad führt.

Mit besten Dank für Ihre Weihnachtsüberraschung,

Ihr

(M. Heckl)

28. Januar 1978

Absstrahlung von einer ringförmig angeregten, sehr biegeweichen, großen Platte

1. Problemstellung

Gegeben sei eine sehr große Platte, die entlang eines Ringes angeregt wird. Die wirkende Kraft soll auf dem ganzen Ring konstant sein, sodass das Problem als radialsymmetrisch betrachtet werden kann.

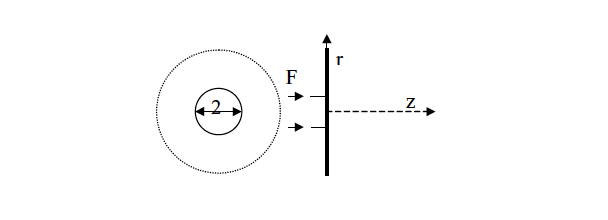
Gesucht ist die Schallabstrahlung von einer solchen Anordnung, wobei insbesondere der Zeitverlauf des Schalldrucks interessiert.

»Zu meiner Überraschung stellte sich dabei heraus, dass das von
Ihnen gewählte Abstrahlprinzip zumindest in der von mir untersuchten
Idealisierung ein zu jedem Zeitpunkt dem Strom entsprechende
Abstrahlung ergibt; d.h. das Einschwingvorgänge und ähnliche
störende Effekte nicht auftreten. «

2. Rechenmodell

Um den mathematischen Aufwand nicht allzu groß werden zu lassen, werden bei der Rechnung folgende Annahmen gemacht:

(a) Die Platte ist so groß und so stark gedaämpft, dass die vom anregenden Ring erzeugten Biegewellen von einer eventuell vorhandenen äußeren Berandung nicht nennenswert reflektiert werden. (Wegen der höheren Dämpfung des Materials dürfte diese Voraussetzung zumindes oberhalb von einigen Hundert Hertz erfüllt sein.)

(b) Auf der Platte kann der Bewegungsgverlauf durch die Biegewellengleichung beschreiben werden; d.h. es dürfen keine Membranspannungen, (die zu Nichtlinearitäten führen würden,) vorhanden sein. (Bei der vorliegenden Konstruktion dürfte diese Voraussetzung erfüllt sein.)

(c) Die Biegewellenlänge der Platte soll bis mindestens 25 kHz kleiner sein als die Luftwellenlänge. (Da das Material sehr weich ist, kann damit gerechnet werden, dass die Biegewellenlänge sogar bis 50 kHz kleiner als die Luftwellenlänge ist.)

(d) Im interessierenden Frequenzbereich - also etwa oberhalb 300 Hz - soll die Strahlungsbelastung durch die umgebende Luft vernachlässigt werden. (Wegen des im Vergleich zu Lautsprechermembranen höheren Gewichts der schwingenden Folie dürfte auch diese Voraussetzung erfüllt sein.)

3. Berechnung des Schalldrucks
3.1. Grundgleichungen

Unter den genannten Voraussetzungen ist das Problem gelöst, wenn es gelingt, die Schallfeldgleichung und die Biegewellengleichung unter Zugrundelegung einer ringförmigen Anregung zu lösen.
Aus der Literatur z. B. Heckl, Acustica 9 (1959) S. 371 ist bekannt, dass für den Schalldruck vor einem sehr großen ebenen Strahler im radialsymmetrischen Fall die Formel gilt:

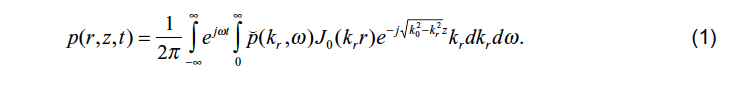
Dabei bedeuten:

Falls die Platte mit der radialsymmetrischen Schnelleverteilung v(r,t) schwingt, dann gilt

mit

ρ0 = Dichte der Luft.

Falls die Platte mit einer radialen Druckverteilung der Form pA(r,t ) erfolgt,
dann gilt

mit

Dabei bedeuten:

Im vorliegenden Fall einer ringförmigen Anregung ist

also

Setzt man (7) in (4) und das Ergebnis in (1) ein, so folgt

Wegen der Voraussetzungen (b) ist im Fernfeld, d. h. ko > kr stets kr << kB, also
 

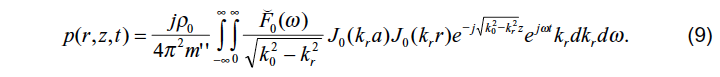
3.2. Auswertung von Gleichung (9)

Berechnet man die Abstrahlung von einer kleinen Kolbenmembran nach den obigen Methoden und dach dem üblichen Verfahren, so läßt sich durch Vergleich zeigen, daß

Streng genommen gilt diese Formel nur, wenn a kleiner ist als die halbe Luftwellenlänge; wenn man sich auf der Mittelsenkrechnten durch den anregenden Ring befindet, gilt Gleichung (10) auch noch für größere Werte von a.
Setzt man (10) in (9) ein, dann ergibt sich

Dieses überraschend einfache Resultat besagt, dass der Zeitverlauf des Schalldrucks in der Nähe der Mittelsenkrechten genau dem Zeitverlauf der auf die Platte wirkenden Kraft und damit dem Zeitverlauf des auf die Schwingspule wirkenden Stroms entspricht. Die Tatsache, dass in der Luft eine Zeitverzögerung erfolgt, kommt im Argument

zum Ausdruck.

4. Schlußfolgerung

Unter den oben gemachten vereinfachenden Annahmen läßt sich theoretisch zeigen, dass der Schalldruck, der von einer großen sehr biegeweichen, gedämpften Platte in der Mittelsenkrechten abgestrahlt wird, in seinem Zeitverlauf genau dem Zeitverlauf der wirkenden Kraft in der Spule (, die sehr leicht sein muss,) und damit dem Zeitverlauf des Spulenstromes entspricht.

Es werden also auch Zeitverläufe des Stromes, die plötzliche Änderungen beinhalten (Rechteckverlauf), im Schalldruckverlauf richtig wiedergegeben.

Der Verlauf des Schalldrucks bei außermittigen Meßpunkten läßt sich au den obigen Formeln nur nach langwierigen numerischen Auswertungen bestimmen. Vermutlich hat der allmähliche Abfall der der Funktion J(kra) für größer werdende Argumente zur Folge, dass bei kleinen Abständen von der Mittelachse erst die 'Ecken im Zeitverlauf abgerundet' werden, und für weiter außermittige Punkte ein ganz anderer Zeitverlauf entsteht.

Download PDF